三年级下册数学是学生从直观思维向抽象逻辑过渡的关键阶段,应用题难度显著提升。以下是口算网系统整理的题型分类及解题技巧,结合教材重点和高频考点,帮助学生高效掌握解题方法:

一、四则运算类应用题
这类问题需灵活运用加减乘除,尤其注重分步分析和数量关系梳理。
1. 连除问题(如分书、分组问题)
题型特征:总量需多次平均分(如“60人先分2队,每队再分3组”)。
解题技巧:
方法1:顺向分步(例:60÷2=30人/队 → 30÷3=10人/组)。
方法2:先求总份数(例:2队×3组=6组 → 60÷6=10人/组)。
易错点:避免跳过中间步骤直接列式(如误用60÷3)。
2. 归一/归总问题
归一问题:先求单一量,再求总量(例:6台拖拉机4小时耕300亩 → 1台1小时耕300÷6÷4=12.5亩 → 8台7小时耕12.5×8×7=700亩)。
归总问题:先求总量,再重新分配(例:原计划每天吃50kg吃30天 → 总粮食1500kg → 实际每天吃60kg → 可吃1500÷60=25天)。
二、数量关系类应用题
需掌握核心公式和关系模型,通过线段图辅助分析。
1. 和差/和倍/差倍问题
和差问题:公式:大数=(和+差)÷2,小数=(和-差)÷2(例:两数和24,差4 → 大数(24+4)÷2=14,小数(24-4)÷2=10)。
和倍问题:公式:较小数=和÷(倍数+1)(例:杏树和桃树共248棵,桃树是杏树3倍 → 杏树248÷(3+1)=62棵)。
差倍问题:公式:较小数=差÷(倍数-1)(例:桃树比杏树多124棵,桃树是杏树3倍 → 杏树124÷(3-1)=62棵)。
技巧:画线段图标注倍数关系,避免混淆“A是B的几倍”与“A比B多几倍”。
2. 平均数问题
核心公式:总数量÷总份数=平均数(例:上午4小时碾米1360kg,下午3小时碾米1096kg → 总米数2456kg ÷ 总时间7小时 ≈ 351kg/小时)。
关键:识别“总数量”与“对应总份数”的匹配关系。
三、特殊情境类应用题
结合生活场景,需灵活建模。
1. 行程问题(相遇问题)
核心公式:
相遇时间=总路程÷速度和
总路程=速度和×相遇时间
例:小红和小明相距500米,小红速度60米/分,小明速度65米/分 → 相遇时间500÷(60+65)=4分钟。
2. 时间与重量问题
时间计算:
分段法:将跨时段问题拆解(例:7:30到9:15 → 7:30-8:00为30分,8:00-9:00为60分,9:00-9:15为15分 → 总时长105分)。
终点减起点法:统一单位计算(例:7:30=450分钟,9:15=555分钟 → 555-450=105分钟)。
重量换算:
口诀:大单位→小单位乘进率,小单位→大单位除以进率(例:2吨300kg=2300kg;1500g=1.5kg)。
3. 方案优化问题
列表法:有序枚举所有可能方案(例:用载重2吨或3吨的车运8吨煤 → 列表对比3吨车2辆、2吨车1辆等组合)。
四、图形与几何题
1. 周长问题
公式:
长方形周长=(长+宽)×2
正方形周长=边长×4
变式题:
靠墙围栏:需减去靠墙边(例:长方形菜地长10米,宽5米,长边靠墙 → 篱笆长度=10+5×2=20米)。
拼组图形:分析拼合后减少的边(例:两个正方形拼成长方形 → 周长比原两个正方形周长和少2条边长)。
高频题型速查表
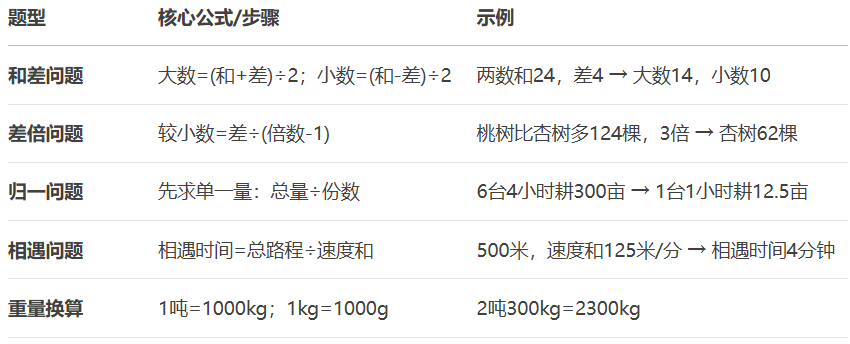
关键解题技巧总结
1. 审题规范:
圈画关键词(如“平均”“倍”“剩”),标注单位(如kg→g需换算)。
2. 建模辅助:
线段图:用于倍数、行程问题。
实物演示:用绳子演示周长问题。
3. 分步拆解:
复杂问题拆为两步(如连除问题),每步标注小标题(例:“先求1队人数”)。
4. 公式逆推:
如周长问题中,已知周长求边长:边长=周长÷4。
口算网学习建议
- 每日一练:重点突破归一、和倍、差倍三类高频题,强化分步列式习惯。
- 错题归因:记录单位未统一、步骤跳跃等常见错误,针对性改进。
- 生活联系:用购物(总价÷数量)、旅行(路程÷时间)等场景理解数量关系。
口算网建议通过系统分类和策略引导,学生可逐步掌握“建模→分步→验证”的解题逻辑,为四年级学习小数、多位数乘除打下坚实基础。






最新评论